PCA (Principal Component Analysis)

PCA (Principal Component Analysis) adalah sebuah teknik dalam analisis data dan reduksi dimensi yang digunakan untuk mengidentifikasi pola tersembunyi dalam dataset yang kompleks. Tujuan utama dari PCA adalah mengurangi dimensi dari dataset yang memiliki banyak fitur (variabel) menjadi ruang dimensi yang lebih rendah tetapi masih mempertahankan sebagian besar informasi yang ada.

Dalam PCA, fitur-fitur dari dataset diterjemahkan ke dalam kombinasi linear baru yang disebut komponen utama (principal components). Komponen utama ini diurutkan berdasarkan tingkat variansnya, dengan komponen pertama memiliki varians tertinggi dan komponen terakhir memiliki varians terendah. Dengan menggunakan komponen utama dengan varians terbesar, PCA membantu mengungkapkan pola-pola penting dalam dataset.

PCA juga dapat digunakan untuk mereduksi dimensi dataset dengan memilih sejumlah komponen utama yang paling signifikan. Dengan mengurangi dimensi, PCA membantu mengatasi masalah overload fitur (curse of dimensionality) dan dapat meningkatkan efisiensi pemrosesan dan visualisasi data.

Selain itu, PCA juga dapat digunakan untuk menghilangkan korelasi antara fitur-fitur dalam dataset, sehingga meningkatkan interpretabilitas dan interpretasi hasil analisis data.

PCA digunakan di berbagai bidang, termasuk analisis data, pengenalan pola, kompresi data, pengolahan citra, dan banyak lagi.

Principal Component Analysis: PCA

import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score


iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis=1)
y_iris = iris['species']

Part number of components

from sklearn.decomposition import PCA
model = PCA(n_components=3)    # 2. Instantiate the model with hyperparameters
model.fit(X_iris)              # 3. Fit to data. Notice y is not specified!

PCA(n_components=3)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Transform the data

X_2D = model.transform(X_iris)
print("show first row of data 3", X_2D[0,:])

show first row of data 3 [-2.68412563  0.31939725 -0.02791483]

print(model.transform(X_iris.iloc[0, :].values.reshape(1, -1)))

[[-2.68412563  0.31939725 -0.02791483]]

C:\Users\LENOVO\AppData\Local\Programs\Python\Python310\lib\site-packages\sklearn\base.py:439: UserWarning: X does not have valid feature names, but PCA was fitted with feature names
  warnings.warn(

Insert X_2D into the original Iris DataFrame

iris['PCA1'] = X_2D[:,0]
iris['PCA2'] = X_2D[:,1]
iris['PCA3'] = X_2D[:,2]
iris.head()

	sepal_length	sepal_width	petal_length	petal_width	species	PCA1	PCA2	PCA3
0	5.1	3.5	1.4	0.2	setosa	-2.684126	0.319397	-0.027915
1	4.9	3.0	1.4	0.2	setosa	-2.714142	-0.177001	-0.210464
2	4.7	3.2	1.3	0.2	setosa	-2.888991	-0.144949	0.017900
3	4.6	3.1	1.5	0.2	setosa	-2.745343	-0.318299	0.031559
4	5.0	3.6	1.4	0.2	setosa	-2.728717	0.326755	0.090079

sns.set()
sns.lmplot(x="PCA1", y="PCA2", hue='species', data=iris, fit_reg=False, height=8, scatter_kws={"s": 150})
sns.lmplot(x="PCA1", y="PCA3", hue='species', data=iris, fit_reg=False, height=8, scatter_kws={"s": 150})
sns.lmplot(x="PCA2", y="PCA3", hue='species', data=iris, fit_reg=False, height=8, scatter_kws={"s": 150})

<seaborn.axisgrid.FacetGrid at 0x2138be0ead0>

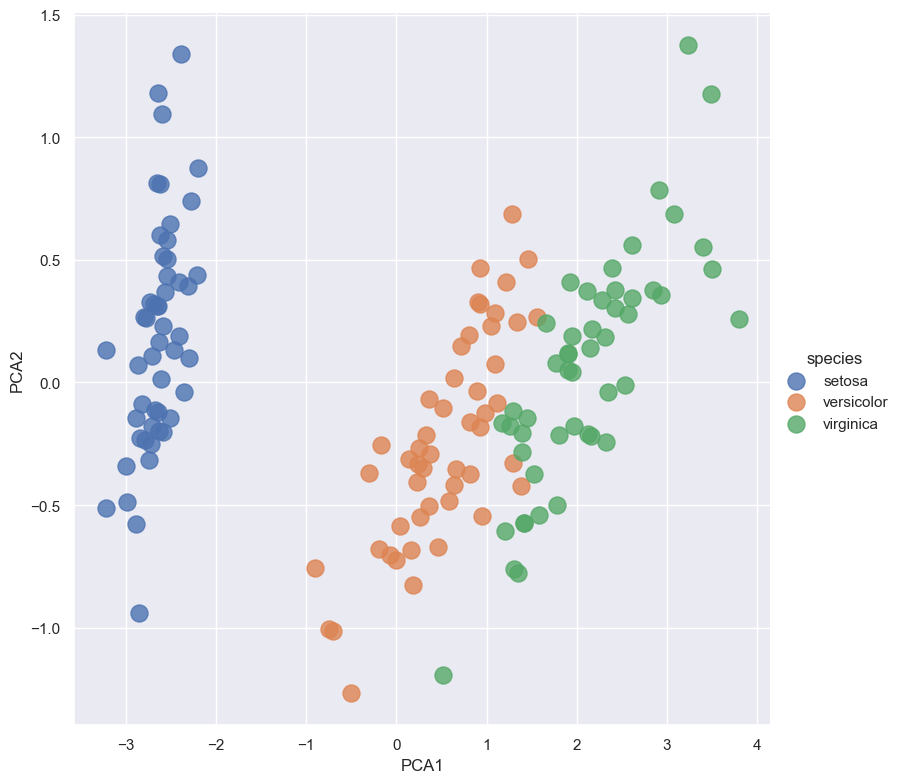
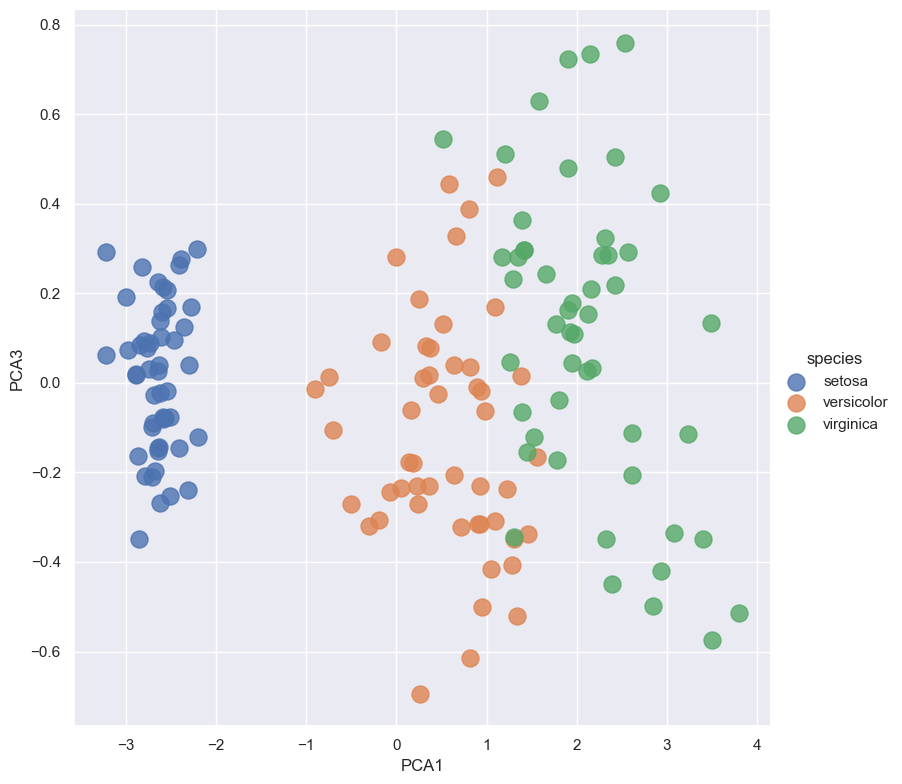
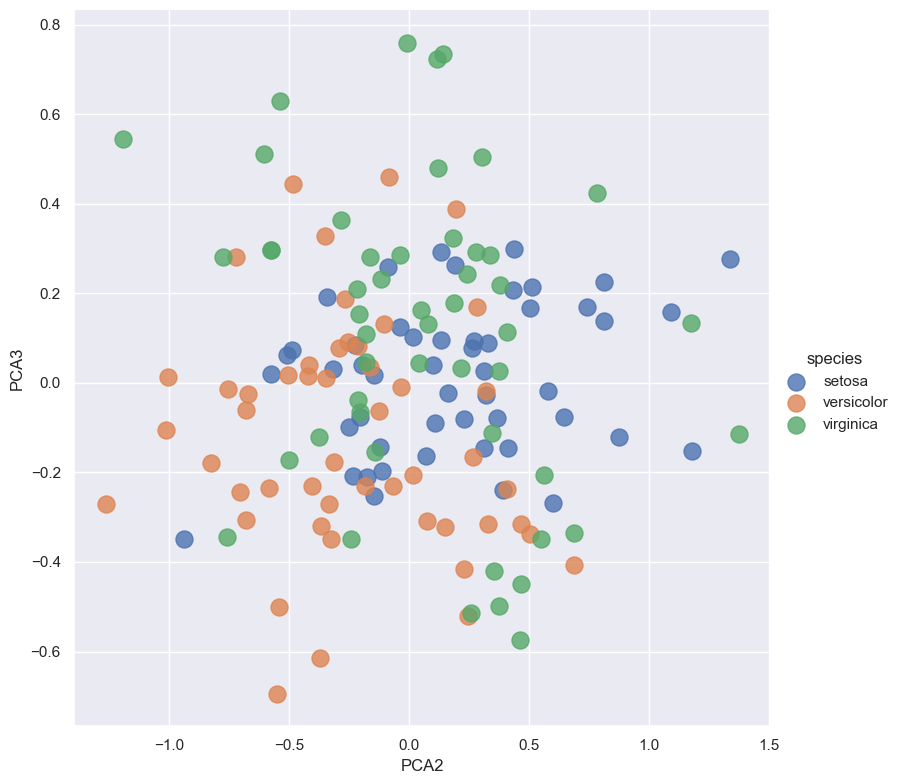
Training new features using Naive Bayes

iris.head()

	sepal_length	sepal_width	petal_length	petal_width	species	PCA1	PCA2	PCA3
0	5.1	3.5	1.4	0.2	setosa	-2.684126	0.319397	-0.027915
1	4.9	3.0	1.4	0.2	setosa	-2.714142	-0.177001	-0.210464
2	4.7	3.2	1.3	0.2	setosa	-2.888991	-0.144949	0.017900
3	4.6	3.1	1.5	0.2	setosa	-2.745343	-0.318299	0.031559
4	5.0	3.6	1.4	0.2	setosa	-2.728717	0.326755	0.090079

from sklearn.model_selection import train_test_split

X_iris = iris.drop('species', axis=1)
y_iris = iris['species']
Xtrain, Xtest, ytrain, ytest = train_test_split(X_iris, y_iris, random_state=1)

Xtrain.head()

	sepal_length	sepal_width	petal_length	petal_width	PCA1	PCA2	PCA3
54	6.5	2.8	4.6	1.5	1.088103	0.074591	-0.307758
108	6.7	2.5	5.8	1.8	2.321229	-0.243832	-0.348304
112	6.8	3.0	5.5	2.1	2.165592	0.216276	0.033327
17	5.1	3.5	1.4	0.3	-2.648297	0.311849	0.026668
119	6.0	2.2	5.0	1.5	1.300792	-0.761150	-0.344995

ytrain.head()

54     versicolor
108     virginica
112     virginica
17         setosa
119     virginica
Name: species, dtype: object

Xtrain = Xtrain[['PCA1', 'PCA2', 'PCA3']]  # Select specific columns using column names

Xtrain.head() 

	PCA1	PCA2	PCA3
54	1.088103	0.074591	-0.307758
108	2.321229	-0.243832	-0.348304
112	2.165592	0.216276	0.033327
17	-2.648297	0.311849	0.026668
119	1.300792	-0.761150	-0.344995

Xtest = Xtest[['PCA1','PCA2','PCA3']]
Xtest.head()

	PCA1	PCA2	PCA3
14	-2.644750	1.178765	-0.151628
98	-0.906470	-0.756093	-0.012600
75	0.900174	0.328504	-0.316209
16	-2.623528	0.810680	0.138183
131	3.230674	1.374165	-0.114548

from sklearn.naive_bayes import GaussianNB # 1. choose model class

model = GaussianNB()                       # 2. instantiate model
model.fit(Xtrain, ytrain)                  # 3. fit model to data

GaussianNB()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

y_model = model.predict(Xtest)  

from sklearn.metrics import accuracy_score

accuracy_score(ytest, y_model)

0.9473684210526315

from sklearn.metrics import confusion_matrix

mat = confusion_matrix(ytest, y_model)

import matplotlib.pyplot as plt
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, cmap='viridis',
            xticklabels=['setosa', 'versicolor', 'virginica'], yticklabels=['setosa', 'versicolor', 'virginica'])

plt.title('Confusion matrix')
plt.xlabel('true label')
plt.ylabel('predicted label');
plt.show()

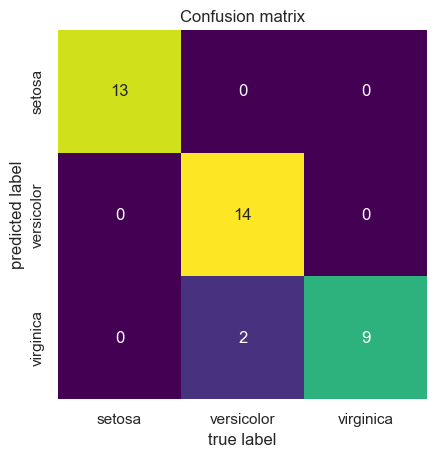
Training new features using KNN

from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

X_train, X_test, y_train, y_test = train_test_split(X_iris, y_iris, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train_scaled, y_train)

KNeighborsClassifier(n_neighbors=3)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

y_pred = knn.predict(X_test_scaled)
y_pred

array(['versicolor', 'setosa', 'virginica', 'versicolor', 'versicolor',
       'setosa', 'versicolor', 'virginica', 'versicolor', 'versicolor',
       'virginica', 'setosa', 'setosa', 'setosa', 'setosa', 'versicolor',
       'virginica', 'versicolor', 'versicolor', 'virginica', 'setosa',
       'virginica', 'setosa', 'virginica', 'virginica', 'virginica',
       'virginica', 'virginica', 'setosa', 'setosa'], dtype=object)

cm = confusion_matrix(y_test, y_pred)
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
cm

Accuracy: 1.0

array([[10,  0,  0],
       [ 0,  9,  0],
       [ 0,  0, 11]], dtype=int64)

df = pd.DataFrame({'Real Values':y_test, 'Predicted Values':y_pred})
df

	Real Values	Predicted Values
73	versicolor	versicolor
18	setosa	setosa
118	virginica	virginica
78	versicolor	versicolor
76	versicolor	versicolor
31	setosa	setosa
64	versicolor	versicolor
141	virginica	virginica
68	versicolor	versicolor
82	versicolor	versicolor
110	virginica	virginica
12	setosa	setosa
36	setosa	setosa
9	setosa	setosa
19	setosa	setosa
56	versicolor	versicolor
104	virginica	virginica
69	versicolor	versicolor
55	versicolor	versicolor
132	virginica	virginica
29	setosa	setosa
127	virginica	virginica
26	setosa	setosa
128	virginica	virginica
131	virginica	virginica
145	virginica	virginica
108	virginica	virginica
143	virginica	virginica
45	setosa	setosa
30	setosa	setosa

Training new features using DecisionTreeClassifier

iris.head()

	sepal_length	sepal_width	petal_length	petal_width	species	PCA1	PCA2	PCA3
0	5.1	3.5	1.4	0.2	setosa	-2.684126	0.319397	-0.027915
1	4.9	3.0	1.4	0.2	setosa	-2.714142	-0.177001	-0.210464
2	4.7	3.2	1.3	0.2	setosa	-2.888991	-0.144949	0.017900
3	4.6	3.1	1.5	0.2	setosa	-2.745343	-0.318299	0.031559
4	5.0	3.6	1.4	0.2	setosa	-2.728717	0.326755	0.090079

from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from imblearn.over_sampling import RandomOverSampler
import pydotplus
from IPython.display import Image

X_train, X_test, y_train, y_test = train_test_split(X_iris, y_iris, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

oversampler = RandomOverSampler()
X_train_resampled, y_train_resampled = oversampler.fit_resample(X_train_scaled, y_train)

# Apply PCA for dimensionality reduction
pca = PCA(n_components=3)
X_train_pca = pca.fit_transform(X_train_resampled)
X_test_pca = pca.transform(X_test_scaled)

clf = DecisionTreeClassifier(max_depth=3, random_state=42)
clf.fit(X_train_pca, y_train_resampled)

DecisionTreeClassifier(max_depth=3, random_state=42)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

y_pred = clf.predict(X_test_pca)
y_pred

array(['versicolor', 'setosa', 'virginica', 'versicolor', 'virginica',
       'setosa', 'versicolor', 'virginica', 'virginica', 'versicolor',
       'virginica', 'setosa', 'setosa', 'setosa', 'setosa', 'versicolor',
       'virginica', 'versicolor', 'versicolor', 'virginica', 'setosa',
       'versicolor', 'setosa', 'virginica', 'virginica', 'virginica',
       'virginica', 'virginica', 'setosa', 'setosa'], dtype=object)

accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

Accuracy: 0.9

from sklearn import tree
feature_names = list(iris.columns[4:]) + ['PCA1', 'PCA2', 'PCA3']
plt.figure(figsize=(10, 8))
tree.plot_tree(clf, feature_names=feature_names, class_names=iris['species'].unique(), filled=True)
plt.show()

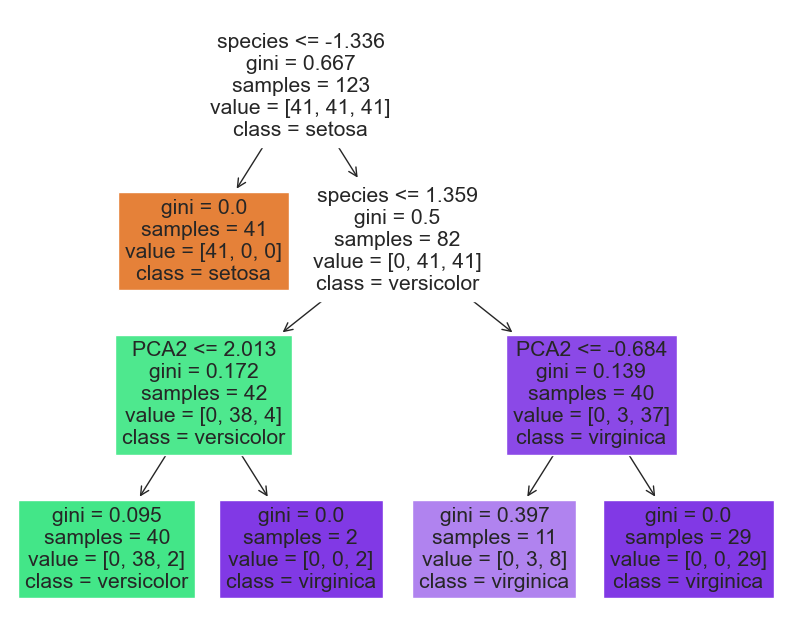
Training new features using ANN

from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X_iris,y_iris, test_size= 0.2, random_state=10)

clf = MLPClassifier(hidden_layer_sizes=(50,50,50), max_iter=1000, alpha=0.0001,
                     solver='sgd', verbose=10,  random_state=21,tol=0.001)
clf

MLPClassifier(hidden_layer_sizes=(50, 50, 50), max_iter=1000, random_state=21,
              solver='sgd', tol=0.001, verbose=10)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

clf.fit(x_train, y_train)
y_pred=clf.predict(x_test)

Iteration 1, loss = 0.86728666
Iteration 2, loss = 0.86098206
Iteration 3, loss = 0.85222217
Iteration 4, loss = 0.84153163
Iteration 5, loss = 0.82954179
Iteration 6, loss = 0.81683062
Iteration 7, loss = 0.80357443
Iteration 8, loss = 0.78987548
Iteration 9, loss = 0.77594874
Iteration 10, loss = 0.76184036
Iteration 11, loss = 0.74767445
Iteration 12, loss = 0.73332399
Iteration 13, loss = 0.71883776
Iteration 14, loss = 0.70445264
Iteration 15, loss = 0.69036337
Iteration 16, loss = 0.67666853
Iteration 17, loss = 0.66326535
Iteration 18, loss = 0.65022063
Iteration 19, loss = 0.63753346
Iteration 20, loss = 0.62514098
Iteration 21, loss = 0.61309085
Iteration 22, loss = 0.60125266
Iteration 23, loss = 0.58958392
Iteration 24, loss = 0.57831021
Iteration 25, loss = 0.56731829
Iteration 26, loss = 0.55677280
Iteration 27, loss = 0.54669231
Iteration 28, loss = 0.53702077
Iteration 29, loss = 0.52765054
Iteration 30, loss = 0.51856010
Iteration 31, loss = 0.50967735
Iteration 32, loss = 0.50097692
Iteration 33, loss = 0.49247871
Iteration 34, loss = 0.48413055
Iteration 35, loss = 0.47585176
Iteration 36, loss = 0.46774864
Iteration 37, loss = 0.45984391
Iteration 38, loss = 0.45216155
Iteration 39, loss = 0.44476416
Iteration 40, loss = 0.43765062
Iteration 41, loss = 0.43078716
Iteration 42, loss = 0.42424354
Iteration 43, loss = 0.41796411
Iteration 44, loss = 0.41194350
Iteration 45, loss = 0.40614151
Iteration 46, loss = 0.40057467
Iteration 47, loss = 0.39520507
Iteration 48, loss = 0.39000779
Iteration 49, loss = 0.38498581
Iteration 50, loss = 0.38013038
Iteration 51, loss = 0.37544592
Iteration 52, loss = 0.37095066
Iteration 53, loss = 0.36664612
Iteration 54, loss = 0.36251537
Iteration 55, loss = 0.35852578
Iteration 56, loss = 0.35465271
Iteration 57, loss = 0.35090005
Iteration 58, loss = 0.34726227
Iteration 59, loss = 0.34370304
Iteration 60, loss = 0.34023124
Iteration 61, loss = 0.33684587
Iteration 62, loss = 0.33355042
Iteration 63, loss = 0.33033796
Iteration 64, loss = 0.32718382
Iteration 65, loss = 0.32410842
Iteration 66, loss = 0.32109964
Iteration 67, loss = 0.31815140
Iteration 68, loss = 0.31527524
Iteration 69, loss = 0.31245286
Iteration 70, loss = 0.30968875
Iteration 71, loss = 0.30698399
Iteration 72, loss = 0.30433234
Iteration 73, loss = 0.30173513
Iteration 74, loss = 0.29918812
Iteration 75, loss = 0.29669001
Iteration 76, loss = 0.29423461
Iteration 77, loss = 0.29181441
Iteration 78, loss = 0.28943569
Iteration 79, loss = 0.28709132
Iteration 80, loss = 0.28479087
Iteration 81, loss = 0.28252632
Iteration 82, loss = 0.28029188
Iteration 83, loss = 0.27809275
Iteration 84, loss = 0.27592413
Iteration 85, loss = 0.27378613
Iteration 86, loss = 0.27168170
Iteration 87, loss = 0.26960635
Iteration 88, loss = 0.26756402
Iteration 89, loss = 0.26555659
Iteration 90, loss = 0.26357277
Iteration 91, loss = 0.26161412
Iteration 92, loss = 0.25968483
Iteration 93, loss = 0.25778468
Iteration 94, loss = 0.25591749
Iteration 95, loss = 0.25407681
Iteration 96, loss = 0.25226598
Iteration 97, loss = 0.25048567
Iteration 98, loss = 0.24872925
Iteration 99, loss = 0.24699901
Iteration 100, loss = 0.24529594
Iteration 101, loss = 0.24361622
Iteration 102, loss = 0.24195976
Iteration 103, loss = 0.24032441
Iteration 104, loss = 0.23871218
Iteration 105, loss = 0.23712112
Iteration 106, loss = 0.23556241

Iteration 107, loss = 0.23402592
Iteration 108, loss = 0.23251041
Iteration 109, loss = 0.23101742
Iteration 110, loss = 0.22954175
Iteration 111, loss = 0.22808382
Iteration 112, loss = 0.22664098
Iteration 113, loss = 0.22521465
Iteration 114, loss = 0.22380676
Iteration 115, loss = 0.22241701
Iteration 116, loss = 0.22105276
Iteration 117, loss = 0.21970923
Iteration 118, loss = 0.21838102
Iteration 119, loss = 0.21706866
Iteration 120, loss = 0.21577152
Iteration 121, loss = 0.21448981
Iteration 122, loss = 0.21322653
Iteration 123, loss = 0.21197804
Iteration 124, loss = 0.21074581
Iteration 125, loss = 0.20953169
Iteration 126, loss = 0.20833190
Iteration 127, loss = 0.20714548
Iteration 128, loss = 0.20597187
Iteration 129, loss = 0.20481136
Iteration 130, loss = 0.20366508
Iteration 131, loss = 0.20253268
Iteration 132, loss = 0.20141358
Iteration 133, loss = 0.20030550
Iteration 134, loss = 0.19920889
Iteration 135, loss = 0.19812358
Iteration 136, loss = 0.19704966
Iteration 137, loss = 0.19598692
Iteration 138, loss = 0.19493597
Iteration 139, loss = 0.19389727
Iteration 140, loss = 0.19286894
Iteration 141, loss = 0.19185159
Iteration 142, loss = 0.19084388
Iteration 143, loss = 0.18984589
Iteration 144, loss = 0.18885871
Iteration 145, loss = 0.18788133
Iteration 146, loss = 0.18691381
Iteration 147, loss = 0.18595718
Iteration 148, loss = 0.18501010
Iteration 149, loss = 0.18407325
Iteration 150, loss = 0.18314615
Iteration 151, loss = 0.18222823
Iteration 152, loss = 0.18132000
Iteration 153, loss = 0.18042027
Training loss did not improve more than tol=0.001000 for 10 consecutive epochs. Stopping.

#Menentukan akurasi
accuracy_score(y_test, y_pred)

1.0

df = pd.DataFrame({'Real Values':y_test, 'Predicted Values':y_pred})
df

	Real Values	Predicted Values
87	versicolor	versicolor
111	virginica	virginica
10	setosa	setosa
91	versicolor	versicolor
49	setosa	setosa
60	versicolor	versicolor
72	versicolor	versicolor
67	versicolor	versicolor
39	setosa	setosa
55	versicolor	versicolor
66	versicolor	versicolor
142	virginica	virginica
53	versicolor	versicolor
1	setosa	setosa
19	setosa	setosa
112	virginica	virginica
85	versicolor	versicolor
38	setosa	setosa
21	setosa	setosa
35	setosa	setosa
102	virginica	virginica
132	virginica	virginica
126	virginica	virginica
24	setosa	setosa
61	versicolor	versicolor
2	setosa	setosa
95	versicolor	versicolor
90	versicolor	versicolor
76	versicolor	versicolor
117	virginica	virginica